| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 노멀 맵핑
- Direct3D12
- 네트워크
- 입방체 매핑
- 게임 디자인 패턴
- Frustum Culling
- 큐브 매핑
- 디퍼드 렌더링
- TCP/IP
- InputManager
- 게임 프로그래밍
- gitscm
- gitlab
- FrameResource
- Deferred Rendering
- Render Target
- 직교 투영
- 네트워크 게임 프로그래밍
- DirectX12
- direct3d
- DirectX
- 장치 초기화
- light
- 조명 처리
- C++
- Dynamic Indexing
- effective C++
- 동적 색인화
- 게임 클래스
- 절두체 컬링
- Today
- Total
코승호딩의 메모장
[Normal Mapping] 본문
이전까지는 조명을 통해 게임 세계를 좀 더 현실감 있게 렌더링 할 수 있었다. 그러나 아쉬웠던 부분은 메쉬에 텍스쳐를 입히면 노멀이 일정하기 때문에 똑같이 빛을 반사한다는 것을 볼 수 있다. 따라서 이번 글에서는 법선 벡터를 사용하여 로우 폴리곤의 그래픽 환경에서 하이 폴리곤의 입체감 및 질감을 구현하는 방법인 노멀 매핑에 대해서 구현한다. 더 나아가 거칠기(Roughness) 값을 단순히 머티리얼 당 상수 버퍼에 사용자가 지정한 값이 아닌 거칠기 맵을 활용 하여 적용하도록 한다.
법선 맵(Normal Map)은 하나의 텍스처에 각 텍셀에 RGB 자료를 담는 것이 아닌 압축된 x, y, z 좌표 성분들을 각 R, G, B 채널에 담은 텍스처이다. 성분당 8비트 총 24비트 이미지 형식을 저장한다고 하면 0~255까지의 1바이트를 담을 수 있다.


위 그림처럼 법선 맵의 텍스처는 전반적으로 파란색을 띠게 되는데 대체로 법선 벡터들은 z 축에 가장 가깝기 때문이다. 따라서 z 축이 저장되어 있는 채널인 B채널의 영향력이 가장 크기 때문에 푸르스름한 모습이 되는 것이다.
그렇다면 하나의 단위벡터를 24비트 형식으로 어떻게 압축을 할 수 있을까? 단위벡터의 모든 성분들은 [-1, 1] 구간에 속한다. 이 값에 0.5를 곱한 뒤 0.5를 더하면 [0, 1] 구간의 값으로 사상되며 이 값에 255를 곱하면 [0, 255]로 사상된다.
그렇다면 반대로 압축을 푸는 방법은 쉽게 할 수 있을 것이다. [0, 255]를 255로 나누고 2를 곱한 다음 1을 빼면 [-1, 1] 구간으로 사상된다. 이 과정은 법선 맵에 담은 정보를 단위 벡터로 불러오기 위해서 필요한 작업이다.
법선 맵을 작성할 때, 법선들을 직접 압축할 필요 없이 Photoshop의 법선 맵 필터를 사용하면 된다. 그러나 법선 맵을 추출하기 위해서는 압축 해제 과정을 쉐이더에서 직접 수행해야 한다.
float3 NormalToWorldSpace(float3 normalMapSample, float3 unitNormalW, float3 tangentW)
{
float3 normalT = 2.0f * normalMapSample - 1.0f;
//...
}다음 코드와 같이 법선 맵을 샘플링한 값을 받으면 되는데 텍스처를 샘플링할 때 이미 Sample 메서드가 [0, 255] 구간의 정수를 255로 나누어서 [0, 1]로 사상하였기 때문에 2를 곱한 다음 1만 빼주면 [-1, 1] 구간으로 사상된다.
텍스처를 메쉬의 삼각형에 입힌다고 할 때, 텍스처 공간에 있는 텍스처는 삼각형이 있는 평면에 접한다. 이 텍스처 좌표계의 기저벡터 T와 B에 삼각형 평면 법선 N을 추가하면 3차원 TBN 기저가 형성된다. 이 공간을 접공간(tangent space)이라고 한다.
조명 공식을 계산하기 위해서는 법선 벡터와 빛이 같은 공간에 있어야 한다. 따라서 가장 먼저 해야 할 일은 접공간 좌표계를 삼각형 정점들이 기준으로 삼은 물체 공간 좌표계와 연관시키는 것이다. 이후 세계 공간 좌표로 이동한다. 좌표계 변환 공식은 다들 알 거라고 가정한다. 이제 접공간의 텍스처를 세계 공간으로 변환해 보자. 우선 정규직교 기저 TBN을 구축해야 한다.
float3 NormalToWorldSpace(float3 normalMapSample, float3 unitNormalW, float3 tangentW)
{
float3 normalT = 2.0f*normalMapSample - 1.0f;
float3 N = unitNormalW;
float3 T = normalize(tangentW - dot(tangentW, N)*N);
float3 B = cross(N, T);
float3x3 TBN = float3x3(T, B, N);
float3 bumpedNormalW = mul(normalT, TBN);
return bumpedNormalW;
}우선 TBN에서 N은 이미 구해진 정보인 삼각형 정점의 월드 좌표계 상 노멀 값이다. 사실 조명계산을 지금은 월드 좌표계 기준으로 했지만 카메라 좌표계 기준으로 해도 상관 없다. 그리고 T를 구해야 하는데 이 공식이 어떻게 나온 지 알아보자.

위 그림을 보면 입력 정점으로 넘어온 tangent 좌표를 월드 변환한 접벡터를 어떠한 공식을 통해 다시 직교시키는 것을 볼 수 있다. 언뜻 보면 어차피 사각형을 만들 때, 법선 벡터와 접벡터를 직교하게 만들었는데 굳이 왜 또 이 과정을 거쳐야 하는지 생각이 들 것이다. 그러나 보간을 거치고 난 뒤 법선 벡터와 접벡터는 더 이상 정규 직교가 아닐 수 있다. 따라서 새롭게 정규 직교 접벡터를 구해야 한다. 우선 법선 벡터는 단위 벡터이다. 그러므로 N과 T를 내적 하면 T를 N에 투영한 점까지의 스칼라 값이 나온다. 이 스칼라 값을 단위 벡터의 N에 곱해주면 N방향을 향하는 투영점까지의 크기가 나온다. 결국 T에서 이 값을 빼면 접선 벡터에 직교하는 접벡터가 나오는 것이다.
마지막으로 B는 간단하게 N과 T를 외적하면 된다. 이제 TBN 벡터들이 모두 만들어졌으니 좌표계 변환을 위한 3x3 행렬을 정의하고 각 순서에 맞게 T, B, N 벡터를 넣으면 TBN 행렬이 완성된다. 이 행렬을 앞서 샘플링한 노멀 맵의 텍스쳐에 곱해주면 접공간의 텍스처 좌표에 있던 텍스처가 아름답게 세계 공간으로 변환된다.
float3 bumpedNormalW = NormalToWorldSpace(normalMap.rgb, pin.normalW, pin.tangentW);
//...
directLight += shadowFactor[i] * ComputeDirectionalLight(gPassConstants.lights[i], mat, bumpedNormalW, toEyeW);이렇게 구한 노멀 값을 조명 계산할 때 넣어주게 되면 기존 노멀 값이 아닌 노멀 맵핑을 위해 변환한 노멀 맵이 완성된다.


왼쪽은 노멀 맵을 사용하지 않은 텍스처이고 오른쪽은 노멀 맵을 사용한 텍스쳐이다. 확실한 차이를 보여주며 그림 같았던 텍스처가 이제 현실감이 좀 생겼다. 이제 거칠기를 직접 조절하지 않고 텍스처로 받아보자.
float roughness = gRoughnessMap.Sample(gsamAnisotropicWrap, pin.uv).x;간단하게 거칠기를 담은 텍스처를 쉐이더에 보내준 후 x, y, z값 중 하나를 거칠기에 넣어준다. 그리고 기존 머티리얼 상수 버퍼에서 거칠기를 넘겨 사용했던 것을 위 거칠기 맵으로 변경해 준다.


왼쪽은 거칠기 맵을 사용하지 않고 모든 픽셀의 거칠기를 0.25f로 준 상황이고 오른쪽은 거칠기 맵을 불러와서 각각의 픽셀마다 다른 거칠기를 가진 상황이다. 크게 변한 것 같지는 않지만 다른 텍스처에서는 놀라운 변화를 보여준다. 그러나 여기서 자세히 보면 이상하게 픽셀이 좀 깨져있는 듯하고 깔끔하지 않은 노멀 벡터를 볼 수 있다.
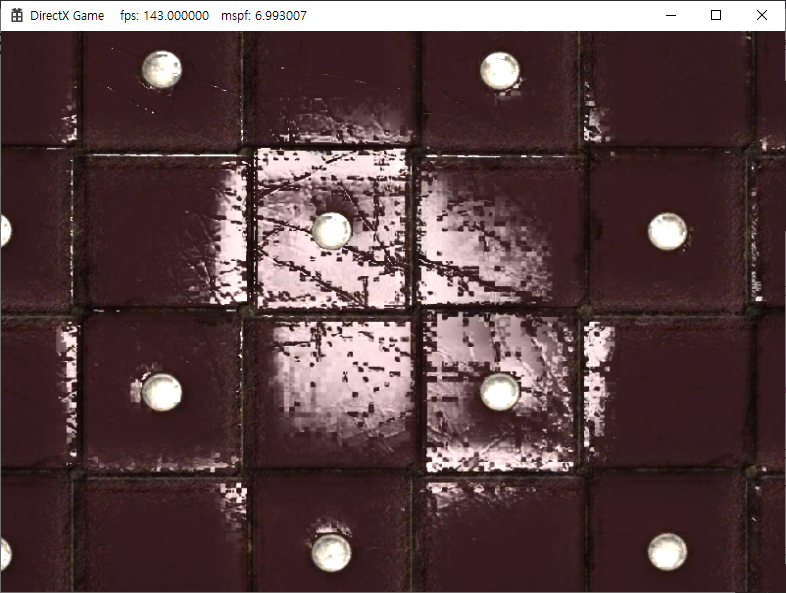

위 그림과 같이 자세히 보거나 멀리 떨어지면 어색하게 점처럼 남아있는 노멀 벡터들을 확인할 수 있다. 어디가 문제일까 곰곰이 생각해 보자. 현재 우리는 dds 파일 즉, 압축 형식의 텍스처를 사용하고 있다. 현재 사용한 텍스처는 BC1의 노멀 맵 텍스처를 사용하는데 노멀 맵의 최상위 품질을 위해서는 BC1이 아닌 BC7 형식의 dds 텍스처를 사용하는 것이 좋다. 이렇게 되면 법선 벡터의 압축에 의한 오차가 크게 줄기 때문이다.


다음은 BC7 노멀 맵을 사용한 텍스처이다. 놀랍게도 차이가 엄청나다. 물론 텍스처의 크기는 BC1에 비해서 BC7이 상당히 크지만 현실적인 렌더링을 위해서는 BC7의 노멀 맵을 사용하는 것이 합당하다고 생각한다.

그런데 예상치 못한 문제가 있었다. 노멀 매핑 조명을 모두 끝난 다음에 구현하였기 때문에 문제를 고친 상황이었지만 조명 처리하는 부분에서 한 가지 삽질을 하였었다. 바로 프레임 레이트가 요동치는 것이다. 이 문제는 컴퓨터에서 실행해 왔었기에 프레임이 노트북에 비해 상대적으로 높아 문제가 없는 줄 알았지만 노트북으로 실행하니 바닥을 쳤다. 어디가 문제인지 디버깅도 해보고 PIX도 돌려본 결과 찾지는 못했지만 결과적으로 ComputeLighting이 문제였다.

기존에 나는 다음과 같이 ComputeLighting이라는 함수에서 조명 타입마다의 함수를 호출하여 반환 값을 누적해서 누적된 값을 반환하였다. 그러나 위 그림처럼 두 함수는 자그마하면서 큰 차이가 있다. 바로 함수에서 넘어오는 gLights의 배열들을 사용했을 때와 상수 버퍼로 넘긴 프레임 당 한번 업데이트되는 조명의 배열을 사용하였을 때이다. 우선 아래 gLights[i] 처럼 함수로 넘긴 배열을 조명 계산에 사용했을 때 프레임 레이트가 굉장히 떨어졌고 위처럼 상수 버퍼의 조명 배열에 바로 접근하였을 때 프레임 레이트가 잘 유지되었다. 결국 문제의 원인은 쉐이더 코드에서는 포인터의 개념이 없기 때문에 정적 배열인 gLights 배열을 최대 크기만큼 복사가 진행되어 모든 정보를 넘겨주는 것이었다. 반대로 위 함수에서는 배열을 따로 넘기지 않고 바로 상수 버퍼의 조명 배열에 접근하였기 때문에 넘기는 과정에서 복사가 일어나지 않은 것이다. 위 방법으로 수정하니 조명 배열의 사이즈가 최대 1000개를 넘기더라도 실행이 잘 되었다.

그 결과 다행히도 프레임 레이트가 정상적으로 올라왔다. 또한 이렇게 만드니 컴퓨터에서 실행하더라도 이전 구현에서는 MaxLights가 100개가 넘어가면 프레임 레이트가 현저히 떨어졌지만 아무리 MaxLights에 100, 1000과 같이 높은 숫자를 넘겨주더라도 문제없이 프레임 레이트를 유지할 수 있었고 노트북에서도 프레임 레이트가 떨어지지 않았다.
처음에 거칠기와 BC1을 사용하여 노멀 매핑을 구현하였을 때까지만 해도 이게 맞나 싶었다. 상당히 결과가 깔끔하지 못했고 프레임 레이트조차 말썽이니 엄청난 혼란을 겪었다. 그러나 하나하나 어디가 문제인지 차근차근 짚어 나갔다. 프레임 레이트가 어디서 문제인지. 주석을 처리해 가며 PIX를 돌려가며 상수 버퍼에 인자는 잘 전달이 되었는지. 만약 for문을 돌 때 상수 버퍼에서 받은 값이 아닌 직접 하드 코딩으로 해서 상수 값을 넣으면 프레임 레이트가 올라가는지. 머티리얼의 문제로 인해 픽셀이 뭉개지는 건지. 이러한 작은 문제들부터 큰 문제까지 침착하게 해결해 나가니 결국 모든 문제는 알지 않고 코드를 구현하였다는 점이다. 만약 책을 보면서 BC1 압축 형식을 BC7로 변경해야 최상의 품질을 나타낸다는 문구를 보지 못했다면 나는 오늘 밤 그리고 일주일 내내 어째서 픽셀이 뭉개지고 결과가 안 좋은 지를 고민했을 것이다. 그래도 결과적으로 노멀 매핑이 아주 성공적이었기 때문에 후회는 없다. 그리고 쉐이더 코드에서 함수로 배열을 넘길 때에는 항상 포인터가 없다는 것과 배열이 복사되어 함수로 넘어간다는 사실을 잊지 말고 꼭 기억하자.
'DirectX12 > DirectX12 응용' 카테고리의 다른 글
| [Dynamic Indexing] (1) | 2023.10.21 |
|---|---|
| [Frustum Culling] (0) | 2023.10.21 |
| [CubeMap] (1) | 2023.10.16 |
| [Light-2] (1) | 2023.10.11 |
| [Light-1] (1) | 2023.10.10 |
| [Resources] (1) | 2023.10.10 |
| [Camera] (1) | 2023.10.09 |




