| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 디퍼드 렌더링
- FrameResource
- Deferred Rendering
- gitscm
- DirectX12
- Dynamic Indexing
- 조명 처리
- InputManager
- 장치 초기화
- 입방체 매핑
- 게임 클래스
- effective C++
- TCP/IP
- 큐브 매핑
- 절두체 컬링
- 게임 프로그래밍
- 게임 디자인 패턴
- 노멀 맵핑
- 직교 투영
- light
- direct3d
- Frustum Culling
- 네트워크 게임 프로그래밍
- 동적 색인화
- 네트워크
- DirectX
- C++
- gitlab
- Direct3D12
- Render Target
- Today
- Total
코승호딩의 메모장
[Arrays] 본문
이번 포스팅에서는 코딩 테스트를 위한 알고리즘, 자료구조들을 다루려고 합니다. 기본 내용들은 코드없는 프로그래밍님의 영상을 기반으로 정리하려고 합니다. 컴퓨터 그래픽스 지식은 어느 정도 있지만 알고리즘 또는 자료구조에 취약한 부분이 있어 보강하고자 공부, 정리 목적으로 글을 올리려고 합니다. LeetCode의 대표적인 문제들을 기반으로 설명하며 LeetCode의 테스트 케이스를 통과하기 위한 목적이 아닌 문제를 풀기 위해 필요한 접근 방법을 기술합니다.
array 배열이란 데이터들이 연속적으로 이어져 random access를 지원하는 자료구조이다. random access란 원소에 색인을 통해 바로 접근하는 것을 가능하게 한다. array의 기본이 되는 문제는 대부분 정렬과 관련이 있다. 이 정렬 알고리즘들을 stable(merge)한 지 unstable(quick, heap)한 지 이용하게 된다. stable 한 것은 만약 같은 값들이 여러 개 존재한다면 정렬을 하였을 때, 이 값의 순서가 유지되는 것을 의미한다. 배열이 만약 정렬이 안되어 있다면 탐색에서 O(n)이 걸리는데 정렬이 되어 있다면 binary search를 사용할 수 있는데 O(logn)이 걸린다.
이렇게 1차원적인 정렬 문제가 나오기도 하지만 2차원 혹은 다차원 문제가 나오기도 한다. 그러나 대부분의 문제는 그래프 쪽에서 많이 나오기 때문에 그래프를 다룰 때 이 문제를 다루도록 하자.
01 Binary search
이진 탐색은 array 문제에서 가장 간단한 기본 문제이다. 배열이 정렬이 되어 있을 때, 원하는 원소를 찾아 달라는 문제이다.
| 1 | 3 | 5 | 6 | 7 | 15 | 20 |
원소들이 정렬이 되어 있기 때문에 다음과 같이 배열에 원소가 들어 있다고 가정하자. 15라는 숫자를 찾고 싶을 때 일반적인 탐색으로 앞에서 부터 하나하나 체크할 수 있으며 O(n)이 걸릴 것이다. 그러나 이진 탐색을 사용하면 O(logn)이 걸린다.
기본 아이디어는 L을 가장 왼쪽 인덱스, R을 가장 오른쪽 인덱스로 시작한다. 루프의 시작에서 pivot을 (L + R) / 2로 업데이트 하고 만약 pivot의 값이 찾고자 하는 값이라면 pivot을 반환하고 작다면 L을 pivot의 오른쪽으로, 크다면 R을 pivot의 왼쪽으로 업데이트한다. 만약 L값이 R의 값보다 커진다면 현재 배열에 찾고자 하는 값이 없다는 뜻이다.
int binary_search(std::array<int, 7> a, int value)
{
int l = 0;
int r = a.size() - 1;
while (l <= r) {
int p = (l + r) / 2;
if (a[p] == value)
return p;
else if (a[p] < value)
l = p + 1;
else
r = p - 1;
}
return -1;
}이진 탐색은 다음과 같이 간단하게 코드로 나타낼 수 있다. L이 R보다 작을 때까지 루프를 돌며 만약 pivot의 값이 찾을 값과 같다면 pivot의 인덱스를 리턴하고 작다면 L을 pivot의 다음 위치로, 크다면 R을 pivot의 이전 위치로 옮긴다.
02 Move zeros
move zeros는 배열 문제의 기본적인 시각을 길러주는 문제이다.
| 0 | 5 | 0 | 7 | 6 | 3 |
위 배열이 주어졌을 때, 0을 제일 끝단으로 보내서 다음과 같이 만들어 주는 문제이다.
| 5 | 7 | 6 | 3 | 0 | 0 |
여기서 중요한 점은 0들이 맨 끝으로 갈 때, 앞의 숫자들은 순서가 변경되지 않아야 한다.
기본 아이디어는 0이 아닌 숫자를 찾아서 왼쪽으로 옮기는 것이다.
void moveZeros(std::array<int, 6>& a)
{
int zIdx{};
for (int idx = 0; idx < a.size(); ++idx) {
if (a[idx] != 0) {
std::swap(a[idx], a[zIdx]);
zIdx++;
}
}
}위 코드의 zIdx는 0이 들어갈 위치의 인덱스이다. 루프를 돌며 0이 아닌 값을 찾았다면 0이 들어가야 할 위치의 a[zIdx]와 현재 위치 a[idx]를 바꾸고 다음 zIdx를 1 증가시킨다.
배열의 맨 앞의 원소에 0이 아닌 숫자가 오더라도 zIdx와 idx가 가리키는 값이 같기 때문에 자기 자신을 스왑해서 문제없다.
03 Find pivot index
| 1 | 8 | 2 | 9 | 2 | 3 | 6 |
이 문제는 pivot의 오른쪽 값들의 합과 왼쪽 값들의 합이 같을 때, 이 pivot을 찾는 문제이다. 위 배열에서는 9 왼쪽의 합이 11이고 오른쪽의 합이 11이므로 9가 pivot이 된다.
기본 아이디어는 슬라이딩이라는 개념을 사용한 것이다. 우선 이 배열의 전체 합을 구한다. 이 전체 합을 rSum이라 하고 위 배열의 첫 원소부터 pivot을 하나씩 증가시켜 가면서 rSum에 pivot의 값을 뺀다. 그리고 pivot의 왼쪽에 있는 값들의 합을 lSum에 저장한다. 만약 rSum과 lSum의 값이 같아진다면 해당 pivot을 반환하면 된다.
int findPivotIndex(std::array<int, 7> a)
{
int rSum = std::accumulate(a.begin(), a.end(), 0);
int lSum{};
int prevNum{};
for (int i = 0; i < a.size(); ++i) {
int num = a[i];
rSum -= num;
lSum += prevNum;
if (rSum == lSum)
return i;
prevNum = num;
}
return -1;
}위 코드를 보면 제일 먼저 rSum에 배열 전체 합을 구한 후 pivot 값을 하나씩 빼준다. 그리고 lSum에는 pivot 이 전의 값을 더한다. 반복하다 rSum과 lSum이 같아지면 해당 인덱스를 반환한다.
슬라이딩 개념을 통해 O(n) 내에 풀 수 있는 문제가 또 있는데 Minimum Size Subarray Sum이라는 문제이다.
| 2 | 3 | 1 | 2 | 4 | 3 |
배열에 다음과 같이 주어졌을 때, 원하는 값 value를 설정하고 부분 배열들을 더했을 때, value값보다 크거나 같은 값 중에 숫자의 개수가 가장 적은 값을 찾는 문제이다. 예를 들어 7이라는 값을 입력하면 {2, 3, 1, 2}, {1, 2, 4}, {4, 3}등이 나올 수 있는데 가장 숫자의 개수가 적은 {4, 3}의 2가 출력으로 나오게 된다.
기본 아이디어는 투 포인터 개념을 사용하는 것이다. 배열의 첫 원소의 인덱스를 가리키는 두 개의 포인터가 있다고 가정할 때, 하나의 포인터는 배열의 원소들을 하나씩 모두 더한다. 그러다가 입력 값보다 커진다면 이때의 숫자 개수를 업데이트한다. 여기서 만약 현재 나아가는 인덱스와 대기 중인 인덱스의 값의 차가 입력 값보다 크다면 대기중인 인덱스를 하나씩 당겨오면서 더한 값에서 빼준다. 이렇게 해야 7보다 크지만 가장 작은 값을 만족할 수 있기 때문이다. 만약 값이 같다면 이 값에 대한 숫자의 개수로 업데이트 하면 될 것이다. 그리고 크다면 계속 대기중인 인덱스를 땡겨오면서 숫자를 빼주면 된다.
int findPivotIndex(std::array<int, 6> a, int value)
{
int sum{};
int cnt{};
int j{};
for (int i = 0; i < a.size(); ++i)
{
sum += a[i];
while (sum - a[j] >= value && j <= i) {
sum -= a[j];
j++;
}
if (sum >= value) {
if (cnt > (i - j + 1) || cnt == 0)
cnt = i - j + 1;
}
}
return cnt;
}04 Sort colors(dutch flag problem)
| 1 | 0 | 2 | 2 | 0 | 1 | 2 | 1 | 0 |
이 문제는 다음과 같이 숫자가 세 가지밖에 없는 배열의 원소들을 정렬하는 문제이다. 이를 정렬하면 다음과 같을 것이다.
| 0 | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 |
만약 sort 함수를 사용하면 O(nlogn)으로 풀 수 있을 것이다. 그러나 문제는 O(n)으로 풀어야 한다. 사실 이 해결법은 간단하다. 배열을 순회하며 각 숫자가 몇 개가 들어 있는지 따로 저장을 해두면 된다. 그리고 마지막 아웃풋에 각 숫자의 개수만큼 추가해 주면 된다. 그러나 또다시 이러한 카운팅 메서드가 아닌 in-place swap을 통해서 문제를 풀어야 한다고 하자. 그렇다면 살짝 어려워질 것이다. in-place swap이란 임시 저장 변수 없이 정렬하는 방식이다.
기본 아이디어는 포인터를 세 개를 두는 것이다. 배열의 첫 원소를 가리키는 포인터와 마지막 원소를 가리키는 포인터와 배열을 순회하는 포인터가 있다고 가정하자. 배열을 순회하는 포인터는 0을 만난다면 첫 원소를 가리키는 포인터와 값을 변경하고 첫 원소를 가리키는 포인터를 1 증가시킨다. 마찬가지로 2를 만난 경우에는 마지막 원소와 값을 변경하고 1 감소시킨다. 다만 이 경우에는 2와 변경된 숫자가 0일 수 있기 때문에 첫 원소를 가리키는 포인터와 체크를 다시 해줘야 한다.
void sortColors(std::array<int, 15>& a)
{
int i{};
int l{};
int r = a.size() - 1;
while (i <= r) {
if (a[i] == 0) {
std::swap(a[i], a[l]);
i++;
l++;
}
else if (a[i] == 2) {
std::swap(a[i], a[r]);
r--;
}
else {
i++;
}
}
}이런 식으로 정렬을 하게 되면 0, 1, 2만 들어 있는 배열을 O(n)에 걸쳐 다른 저장 공간 없이 정렬이 가능하다. 문제의 핵심 원리가 quick sort의 원리와 크게 다르지 않은 partion 문제이다.
05 Merge sorted array
| 1 | 3 | 5 | 0 | 0 | 0 |
| 2 | 4 | 8 |
이 문제는 정렬이 되어 있는 array를 합치는 문제이다. 위 두 번째 배열을 첫 번째 배열에 합쳐야 하는 것인데 각각 숫자가 몇 개가 들어 있는지 변수에 따로 저장하고 있다. m을 첫 번째 배열의 숫자 개수라고 한다면 3(0 제외)이고 n을 두 번째 배열의 숫자 개수라고 한다면 3이다. 이 문제는 새로운 배열에 두 배열을 비교해 가며 작은 숫자를 하나씩 넣어주면 쉽게 풀 수 있을 것이다. 그러나 문제에서 원하는 것은 새로운 배열에 만드는 것이 아니라 첫 번째 배열에 합쳐 주는 것이다. 따라서 첫 번째 배열은 다음과 같이 결과가 나와야 한다.
| 1 | 2 | 3 | 4 | 5 | 8 |
기본 아이디어는 두 배열을 뒤에서부터 비교하며 큰 숫자를 찾아 첫 번째 배열의 마지막부터 하나씩 채워주는 것이다.
void mergeSort(std::array<int, 6>& a, int m, std::array<int, 3>& b, int n)
{
int ap = m - 1;
int bp = n - 1;
int i = a.size() - 1;
while (bp >= 0 && ap >= 0) {
if (a[ap] >= b[bp]) {
a[i] = a[ap];
ap--;
}
else {
a[i] = b[bp];
bp--;
}
i--;
}
if(bp >= 0)
memcpy(a.data(), b.data(), sizeof(int) * (bp + 1));
}
코드는 간단하지만 한 가지 중요한 점은 이 while 루프는 둘 중 하나가 음수가 되면 바로 빠져나오기 때문에 만약 첫 번째 배열이 모든 숫자가 두 번째 배열보다 더 크다면 결국 bp는 하나도 바뀌지 않은 채 루프 문을 벗어날 것이다. 따라서 이 경우 bp에 남아 있는 모든 원소들을 a 배열의 남은 부분에 복사해야 한다.
이렇게 인덱스를 통해 접근하는 사고방식이 매우 중요하다. 인덱스를 어떻게 사용해야 할지 안다면 array 문제는 모두 풀 수 있다.
06 Find peak element
| 1 | 2 | 3 | 5 | 4 |
| 1 | 3 | 2 | 4 | 5 | 7 | 6 |
이 문제는 어떤 배열이 있을 때, peak element를 찾는 문제이다. peak element는 어떤 숫자가 이웃 숫자보다 클 때 peak라고 정의한다. 예를 들어 첫 번째 배열에서 5는 이웃 숫자인 3과 4보다 크기 때문에 5의 인덱스인 3을 반환한다. 두 번째 배열에서는 3, 7이 peak element이기 때문에 둘 중 하나를 반환하면 성공이다. O(n)에 찾기 위해서는 그냥 배열을 돌며 주위 숫자를 비교하며 찾으면 될 것이다. 그러나 O(n)보다 빨리 찾아야 된다면 어떻게 해야 할까?
기본 아이디어는 O(n)보다 빠른 O(logn)인 binary search를 사용하는 것이다. 첫 번째 배열을 예를 들면 (L + R) / 2의 인덱스에 해당하는 pivot 3은 다음 인덱스인 5보다 작으므로 peak 후보는 오른쪽에 있을 수 있다. 따라서 L을 가운데의 다음 값으로 업데이트 한다. 다음 pivot은 5가 되며 다음 인덱스와 비교를 한다. 다음 인덱스에 해당하는 값인 4보다 크기 때문에 해당 피봇이 peak element 이다.
int findPeakElem(std::array<int, 7>& a)
{
int l = 0;
int r = a.size() - 1;
while (l < r){
int pivot = (l + r) / 2;
int curNum = a[pivot];
int nextNum = a[pivot + 1];
if (curNum < nextNum) l = pivot + 1;
else r = pivot;
}
if (l == a.size() - 1)
return -1;
return l;
}
이러한 문제들은 다음과 같이 그래프를 그리면서 풀면 쉽다.
배열 {1, 2, 3, 5, 4}에서 peak element를 찾는다고 한다면 직관적으로 다음과 같이 그래프를 그릴 수 있다. 처음 배열을 반으로 나누고 이 때, pivot의 값과 다음 숫자를 비교하여 더 크기 때문에 peak는 오른쪽에서 일어난다는 것을 알 수 있다. 업데이트 후 그 다음 숫자가 더 작기 때문에 peak는 왼쪽에서 일어난다는 것을 알 수 있다. 이렇게 L과 R이 만나게 되며 생기는 곳이 peak인 것이다.
이렇게 문제를 그림으로 나타내어 솔루션을 생각하는 것도 방법이 될 수 있다.
07 Merge intervals
이 문제는 [1, 5] [3, 7] [10, 15] [8, 16]과 같은 interval들이 주어 졌을 때, interval들을 전부 합쳐서 시작과 끝 점으로 나타내는 것이다. 위 예시에서는 [1, 7] [8, 16]과 같은 결과를 출력하면 된다. 그렇다면 앞의 find peak element에서 사용했던 방법처럼 그림을 그려서 풀어보도록 하자.

위 interval들을 선으로 나타내 보면 다음과 같다. 해결법은 언뜻 보기에 새로운 merge를 할 때마다 기존 interval들과 비교를 하는 O(n^2)을 생각해낼 수 있다. 그러나 더 좋은 방법을 찾아야 한다. 따라서 O(nlogn) 즉 정렬을 사용하는 문제 풀이를 시도해볼 수 있다. 그렇다면 다음으로 이 interval들을 정렬을 해보자.

이처럼 정렬을 사용하게 되면 다음 그림과 같아질 것이고, 이 그림에서 우리는 한 번의 순회만으로 해결할 수 있다.
기본 아이디어는 우선 interval들을 정렬을 한 뒤 start 인덱스와 end 인덱스를 첫 번째 interval로 설정한다. 만약 end가 다음 interval의 start보다 크고 다음 interval의 end보다 작다면 새로운 end는 다음 interval의 end가 된다. 그러나 만약 end가 다음 interval의 start보다 작다면 새로운 start를 생성해야 한다. 따라서 반환해야 할 배열에 기존 merge interval을 저장해 두고 다음 interval의 start가 새로운 start가 된다. 이렇게 반복하면 된다. 그러나 주의할 점은 [8, 16] [10, 15] 처럼 앞의 interval이 뒤의 interval을 모두 cover하는 경우가 생긴다면 continue를 통해 넘어가야 할 것이다.
std::vector<std::pair<int, int>> mergeIntervals(std::vector<std::pair<int, int>>& a)
{
std::vector<std::pair<int, int>> ans;
std::sort(a.begin(), a.end(), [](const std::pair<int, int>& l, const std::pair<int, int>& r) {
return l.first < r.first;
});
int first = a[0].first;
int end = a[0].second;
for (int i = 1; i < a.size(); ++i) {
auto cur = a[i];
if (end > cur.first && end < cur.second)
end = cur.second;
else if (end > cur.first && end > cur.second)
continue;
else {
first = cur.first;
end = cur.second;
}
ans.emplace_back(first, end);
}
return ans;
}이렇게 정렬을 한 뒤 해결하게 되면 시간 복잡도는 O(n) + O(nlogn)이 된다.
08 Shortest unsorted continuous subarray
| 2 | 5 | 7 | 6 | 3 | 9 | 15 |
이 문제는 주어진 배열을 오름차순으로 정렬을 할 때, 부분 배열을 정렬을 하면 전체 정렬 배열이 된다. 예를 들어 위 배열에서 부분 배열 {5, 7, 6, 3}을 정렬하면 전체가 정렬되게 된다. 그리고 부분 배열의 길이 4를 반환하면 된다. 만약 이미 정렬이 되어 있는 상태라면 0을 반환하면 되는데 여기서 한 가지 확인해야 할 점은 부분 배열의 길이가 최소가 되어야 한다.
이 문제를 과연 O(n)만에 풀 수 있을까? 그렇다. 일단 그림을 먼저 그려보도록 하자

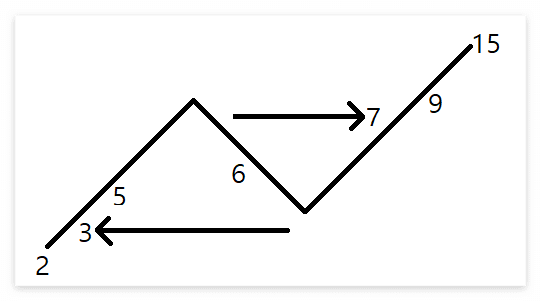
기본 아이디어는 다음의 그림을 이용한다. 우선 꺾인 후 최솟값을 먼저 찾는다. 위 그림에선 3이 최솟값이다. 찾았다면 3을 옆으로 그어보자. 그렇다면 3의 위치는 2의 다음이 될 것이다. 똑같이 꺾인 후의 최댓값을 찾아서 옆으로 그으면 다음과 같이 각각 최대 최솟값의 인덱스를 구할 수 있을 것이다. 그렇다면 이제는 인덱스를 구하여 계산만 해주면 내부 부분 배열의 원소들의 개수가 나올 것이다.
int shortestUnsortedContinuousSubArray(std::array<int, 9> a)
{
int subArrayStartValue = std::numeric_limits<int>::max();
int subArrayEndValue = std::numeric_limits<int>::min();
for (int i = 1; i < a.size() - 1; ++i) {
int num = a[i];
int prevNum = a[i - 1];
int nextNum = a[i + 1];
if (num < prevNum && num < nextNum)
if (num < subArrayStartValue)
subArrayStartValue = num;
if (num > prevNum && num > nextNum)
if (num > subArrayEndValue)
subArrayEndValue = num;
}
int subArrayStartIdx{};
int subArrayEndIdx{};
for (int i = 1; i < a.size() - 1; ++i) {
if (subArrayStartValue > a[i - 1] && subArrayStartValue < a[i])
subArrayStartIdx = i;
if (subArrayEndValue > a[i] && subArrayEndValue < a[i + 1])
subArrayEndIdx = i;
}
return (subArrayStartIdx == 0) ? 0 : (subArrayEndIdx - subArrayStartIdx + 1);
}우선 부분 배열의 시작 숫자와 끝나는 숫자를 구해야 한다. 루프를 돌며 이전 값과 이후 값을 비교하여 만약 이전, 이후 값이 해당 값보다 작다면 그 값은 최댓값이 될 것이고 크다면 최솟값이 될 것이다. 그 다음 루프에서 적절한 위치를 찾아서 인덱스를 찾아 계산을 통해 반환하면 된다. 이렇게 최댓값과 최솟값을 찾는데 걸리는 시간 O(n)과 최댓값과 최솟값의 인덱스를 찾는데 걸리는 시간 O(n)이기 때문에 결과적으로 O(n)만에 부분 배열의 인덱스를 구할 수 있었다.
09 Find a duplicate number
이 문제는 만약 1~n의 숫자가 들어 있는 배열이 있다고 하였을 때, 각 숫자는 한 개씩 들어 있고 추가로 하나의 숫자가 들어오며 총 n+1개의 숫자가 들어 있는 배열이 된다. 이 때, 추가로 들어간 하나의 숫자를 찾는 문제이다.
| 1 | 2 | 3 | 4 | 2 |
위 배열에서는 {1, 2, 3, 4} 배열에서 추가로 2가 들어온 상태이다. 이 때, 총 5개의 숫자 중 추가로 들어온 2를 찾는 문제이다. 해결 방법으로는 O(n^2)을 통해 루프를 두 번 돌며 쉽게 구할 수 있다. 그러나 만약 이보다 빠른 해결법을 찾기 위해선 어떻게 해야 할까?
먼저 정렬을 하는 것이다. 정렬을 한 후 두 개의 인접한 포인터를 하나씩 올려가며 값이 같은 지 비교하는 것이다. 그렇다면 정렬하는데 O(nlogn)과 루프를 돌며 인접한 숫자를 찾는데 O(n)으로 총 O(nlogn) + O(n)이 걸릴 것이다. 그렇다면 이보다 더 빠른 O(n)으로만 찾을 수 있는 방법이 있을까?
새로운 카운팅 배열을 만들어서 루프를 돌며 하나씩 개수를 저장한다. 만약 이미 있다면 반환해주면 된다. 그렇다면 만약 또 여기서 O(n)의 시간 복잡도는 만족했지만 O(n)의 공간 복잡도는 어떻게 해결할 수 있을까? sweep을 사용하는 것이다.
기본 아이디어는 이전에 설명한 새로운 배열을 만들어서 저장하는 것이 아닌 입력 받은 배열 자체를 인덱스를 담은 배열로 보는 것이다. 예를 들어서 {1, 2, 3, 4, 2}의 배열에서 [0]에 해당하는 1의 값은 인덱스 1이라는 의미이다. 이렇게 인덱스를 저장한 배열로 생각하고 해당 인덱스로 넘어가 값에 -1을 곱해주게 되면 결국 인덱스로 넘어간 값이 음수라면 반환해주면 되는 것이다.
int FindDuplicateNumber(std::array<int, 5>& a)
{
for (int i = 0; i < a.size(); ++i) {
int& targetIndex = a[i];
int& checkValue = a[abs(targetIndex)];
if (checkValue < 0)
return abs(targetIndex);
checkValue *= -1;
}
}위 코드에서 targetIndex는 현재 인덱스의 배열 값이며 즉, 음수로 변경할 배열 인덱스를 의미한다. 그리고 checkValue는 targetIndex에 해당하는 인덱스를 가진 배열의 값이다. 따라서 checkValue가 음수라면 targetIndex를 반환하면 된다.
10 2sum 3sum 4sum
이 문제는 array에서 가장 유명한 문제이다. 우선 2sum부터 살펴보면, {1, 3, 7, 4, 8}의 배열이 있을 때, 두 수의 합이 target이 되는 값을 찾는 것이다. 만약 target이 5라면 {1, 4}가 필요하기 때문에 반환 값은 인덱스에 해당하는 {0, 3}이다. 단순히 루프를 두 번 돌아서 target과 값이 같다면 반환하는 방법은 O(n^2)이기 때문에 다른 방법을 사용해야 한다. 그렇다면 O(nlogn)을 고려해볼 수 있을 것이다. 바로 정렬을 사용하는 것이다.
정렬을 하게 되면 {1, 3, 4, 7, 8}이 되고 여기서 두 개의 포인터 L과 R을 사용하는 것이다. L은 배열의 맨 왼쪽, R은 배열의 맨 오른쪽을 가리킨다. 이 때 L + R 이 target이 되는지 확인하고 만약 target보다 작다면 R을 왼쪽으로 하나씩 이동하며 L+R을 업데이트 하고 작다면 L을 오른쪽으로 이동하며 업데이트 한다. 이 방법은 정렬시 O(nlogn), 루프에서 O(n)이 걸린다. 만약 정렬이 이미 되어 있는 상태라면 위 방법이 유리할 것이다.
다음은 2sum의 해결 코드이다.
std::vector<int> TwoSum(std::array<int, 5>& a, int target)
{
std::sort(a.begin(), a.end());
std::vector<int> ans;
int l = 0;
int r = a.size() - 1;
while (l < r) {
if (a[l] + a[r] == target) {
ans.emplace_back(l);
ans.emplace_back(r);
return ans;
}
if (a[l] + a[r] < target)
l += 1;
else if (a[l] + a[r] > target)
r -= 1;
}
}
다음은 3sum의 해결 코드이다.
std::vector<std::vector<int>> threeSum(std::array<int, 15>& a, int targetNum)
{
std::sort(a.begin(), a.end());
std::vector<std::vector<int>> ans;
for (int i = 0; i < a.size() - 1; ++i) {
if (i > 0 && a[i] == a[i - 1])
continue;
int l = i + 1;
int r = a.size() - 1;
while (l < r) {
int sum = a[i] + a[l] + a[r];
if (sum < targetNum)
l++;
else if (sum > targetNum)
r--;
else {
ans.emplace_back(std::vector<int>{a[i], a[l], a[r]});
while (l + 1 < a.size() && a[l + 1] == a[l])
l++;
while (r - 1 >= 0 && a[r - 1] == a[r])
r--;
l++;
r--;
}
}
}
return ans;
}만약 I, L, R의 현재 값이 다음 루프에서 나올 값과 같다면 [0, -1, 1] [0, -1, 1]과 같이 중복된 값이 나올 것이다. 이를 방지하기 위해 I 값은 0보다 클 경우 이전 값과 같다면 continue를 통해 넘어간다. 그리고 L과 R은 다음 같은 값이 나오지 않을 때까지 while문을 통해 증가시켜줘야 한다. 나머지는 2sum과 크게 다른 것이 없다. 4sum도 마찬가지로 하나 더 늘리면 될 것이다.
11 Rotate image
1차원 배열과 2차원 배열의 사용은 다들 잘 알고 있을 것이다. 이러한 2차원 배열은 이미지에서도 사용할 수 있는데 예를 들어 500x300 크기의 이미지가 있다면 image[300][500]과 같을 것이다. 만약 한 첫 번째 픽셀이 하얀색이라면 image[0][0] = 255 일 것이고 두 번째 픽셀이 검은색이라면 image[0][1] = 0 이 된다. 이러한 이미지 배열에 대한 Indexing, flippinf, rotating과 같은 문제가 나올 수 있다. 이번엔 rotating에 대해서 알아볼 것이다.
| 4 | 5 | 6 |
| 9 | 2 | 3 |
| 1 | 7 | 8 |
| 1 | 9 | 4 |
| 7 | 2 | 5 |
| 8 | 3 | 6 |
위와 같은 3x3 배열이 주어질 때 다음과 같이 90도를 회전하여 배열을 변경해야 하는 문제이다. 초급 난이도로 푸는 방법은 for문을 두 번 돌아 oldX, oldY를 이용하여 newX, newY를 정의하면 될 것이다. 예를 들어 newY = oldX가 될 것이다. 그리고 newX = -oldY + 2가 될 것이다. 실제로 계산해보면 나올 것이다. 이렇게 정의가 되었다면 newImage[newY][newX] = oldImage[Y][X]로 새로운 이미지 배열을 구할 수 있을 것이다. 그렇다면 새로운 배열을 사용하지 않고 어떻게 해결할 수 있을까?
